kohigowild
221121 :: [leetcode] Apply Operations to an Array, Longer Contiguous Segments of Ones than Zeros, Search a 2D Matrix II 본문
221121 :: [leetcode] Apply Operations to an Array, Longer Contiguous Segments of Ones than Zeros, Search a 2D Matrix II
kohi ☕ 2022. 11. 21. 14:22Apply Operations to an Array
You are given a 0-indexed array nums of size n consisting of non-negative integers.
You need to apply n - 1 operations to this array where, in the ith operation (0-indexed), you will apply the following on the ith element of nums:
- If nums[i] == nums[i + 1], then multiply nums[i] by 2 and set nums[i + 1] to 0. Otherwise, you skip this operation.
After performing all the operations, shift all the 0's to the end of the array.
- For example, the array [1,0,2,0,0,1] after shifting all its 0's to the end, is [1,2,1,0,0,0].
Return the resulting array.
Note that the operations are applied sequentially, not all at once.
Example 1:
Input: nums = [1,2,2,1,1,0]
Output: [1,4,2,0,0,0]
Explanation: We do the following operations:
- i = 0: nums[0] and nums[1] are not equal, so we skip this operation.
- i = 1: nums[1] and nums[2] are equal, we multiply nums[1] by 2 and change nums[2] to 0. The array becomes [1,4,0,1,1,0].
- i = 2: nums[2] and nums[3] are not equal, so we skip this operation.
- i = 3: nums[3] and nums[4] are equal, we multiply nums[3] by 2 and change nums[4] to 0. The array becomes [1,4,0,2,0,0].
- i = 4: nums[4] and nums[5] are equal, we multiply nums[4] by 2 and change nums[5] to 0. The array becomes [1,4,0,2,0,0].
After that, we shift the 0's to the end, which gives the array [1,4,2,0,0,0].
Example 2:
Input: nums = [0,1]
Output: [1,0]
Explanation: No operation can be applied, we just shift the 0 to the end.
Constraints:
- 2 <= nums.length <= 2000
- 0 <= nums[i] <= 1000
배열의 앞 값과 뒤 값이 똑같으면 앞 값에는 2를 곱하고 뒤 값은 0으로 만듦
마지막 최종 배열에서 0을 뒤로 전부 밀어서 반환
Solution:
/**
* @param {number[]} nums
* @return {number[]}
*/
var applyOperations = function (nums) {
for (let i = 0; i < nums.length; i++) {
if (nums[i] == nums[i + 1]) {
[nums[i], nums[i + 1]] = [nums[i] * 2, 0];
}
}
const moveZeros = (next, curr) => {
if (curr !== 0) return 0;
return curr - next;
};
return nums.sort(moveZeros);
};
Longer Contiguous Segments of Ones than Zeros
Given a binary string s, return true if the longest contiguous segment of 1's is strictly longer than the longest contiguous segment of 0's in s, or return false otherwise.
- For example, in s = "110100010" the longest continuous segment of 1s has length 2, and the longest continuous segment of 0s has length 3.
Note that if there are no 0's, then the longest continuous segment of 0's is considered to have a length 0. The same applies if there is no 1's.
Example 1:
Input: s = "1101"
Output: true
Explanation:
The longest contiguous segment of 1s has length 2: "1101"
The longest contiguous segment of 0s has length 1: "1101"
The segment of 1s is longer, so return true.
Example 2:
Input: s = "111000"
Output: false
Explanation:
The longest contiguous segment of 1s has length 3: "111000"
The longest contiguous segment of 0s has length 3: "111000"
The segment of 1s is not longer, so return false.
Example 3:
Input: s = "110100010"
Output: false
Explanation:
The longest contiguous segment of 1s has length 2: "110100010"
The longest contiguous segment of 0s has length 3: "110100010"
The segment of 1s is not longer, so return false.
Constraints:
- 1 <= s.length <= 100
- s[i] is either '0' or '1'.
이진법 문자열이 주어졌을 때, 1이 연속하는 가장 긴 길이가 0이 연속하는 가장 긴 길이보다 길면 true
그렇지 않으면 false 반환
/**
* @param {string} s
* @return {boolean}
*/
var checkZeroOnes = function (s) {
let ones = 0;
let zeroes = 0;
let maxOnes = 0;
let maxZeroes = 0;
for (let char of s) {
if (char === "1") {
ones++;
zeroes = 0;
} else {
zeroes++;
ones = 0;
}
maxOnes = Math.max(maxOnes, ones);
maxZeroes = Math.max(maxZeroes, zeroes);
}
return maxOnes > maxZeroes;
};
Search a 2D Matrix II
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
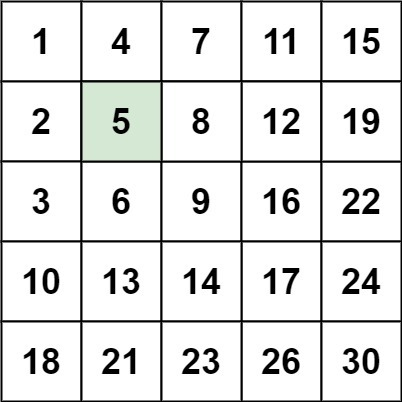
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true
Example 2:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= n, m <= 300
- -109 <= matrix[i][j] <= 109
- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
- -109 <= target <= 109
Solution:
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
var searchMatrix = function (matrix, target) {
let i = matrix.length - 1;
let j = 0;
while (i >= 0 && j < matrix[0].length) {
if (matrix[i][j] > target) {
i--;
} else if (matrix[i][j] < target) {
j++;
} else {
return true;
}
}
return false;
};




